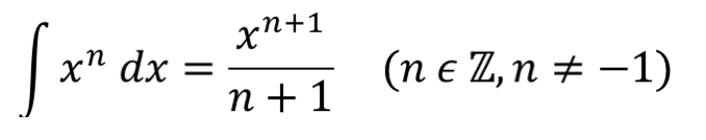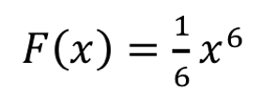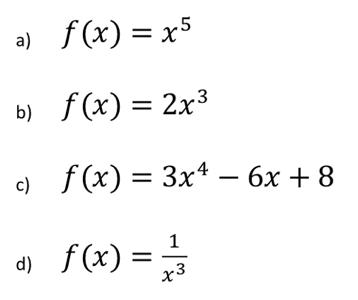Einführung in die Integralrechnung
Eine grundlegende Aufgabe der Differentialrechnung ist es, zu einer gegebenen Funktion f ihre Ableitungsfunktion f’ zu bestimmen. Beim Aufsuchen von Flächeninhaltsfunktionen bzw. Bestandsfunktionen stellte sich uns die umgekehrte Aufgabe: Gegeben ist eine Funktion f.’ Gesucht ist diejenige Funktion f deren Ableitung die gegebene Funktion f’ ist. Die Integralrechnung beschäftigt sich mit genau dieser Frage.
Wir erweitern die Integralrechnung nun durch einen weiteren Begriff:
Die Flächeninhaltsfunktion bzw. die Bestandsfunktion ist dabei eine Stammfunktion von f. Alle anderen Stammfunktionen unterscheiden sich nur noch um die additive Konstante c.
Man bezeichnet den Vorgang des Aufsuchens von Stammfunktionen als Integration. Es handelt sich dabei um die Umkehrung der Differentation. Die Menge aller Stammfunktionen einer gegebenen Funktion f bezeichnet man als unbestimmtes Integral von f und verwendet die symbolisierte Schreibweise:
Das Adjektiv unbestimmt drückt aus, dass das Ergebnis wegen des Auftretens der Integrationskonstante c nicht eindeutig bestimmt ist. (Siehe Auffinden der Bestandsfunktion)
Das Integralzeichen stellt ein stilisiertes „S“ dar und steht für „Summe“. Das „dx“ steht für die unendlich kleine Breite eines Rechtecks, wenn n gegen unendlich geht, wie wir es bei der Arbeit mit Ober- und Untersumme gemacht haben. Diese Schreibweise soll verdeutlichen, dass es sich beim bestimmten Integral um den Grenzwert einer Summe von Produkten handelt.
Definition Stammfunktion
Jede differenzierbare Funktion F, für die F’(x)=f(x) gilt, wird als Stammfunktion von f bezeichnet. Zu einer Funktion f gibt es viele Stammfunktionen, die sich nur um eine Konstante unterscheiden.
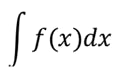
Bei der Erarbeitung der Flächeninhaltsfunktion bzw. Bestandsfunktion hast du bereits einen Zusammenhang entdeckt, der zwischen Ursprungsfunktion und zugehöriger Bestandsfunktion besteht. Dieser Zusammenhang besteht dementsprechend auch zwischen einer Funktion und ihrer Stammfunktion. Für Potenzfunktionen gilt in der Integralrechnung also ebenfalls wie in der Differentialrechnung die Potenzregel:
Beispiele:
Bestimme die Menge aller Stammfunktionen von f. Gesucht st also das unbestimmte Integral von f.