Wir sind immer noch dabei unser Hauptanliegen zu klären. Wir wollen, den Inhalt einer durch den Graphen einer Funktion begrenzten Fläche bestimmen. Diese Fläche nennt man auch Integral.

Im Folgenden werden wir erkennen, dass man den Flächeninhalt zwischen dem Graphen einer differenzierbaren Funktion f und der x-Achse über einem Intervall [a; b] recht einfach bestimmen kann, wenn man eine Stammfunktion F von f kennt.

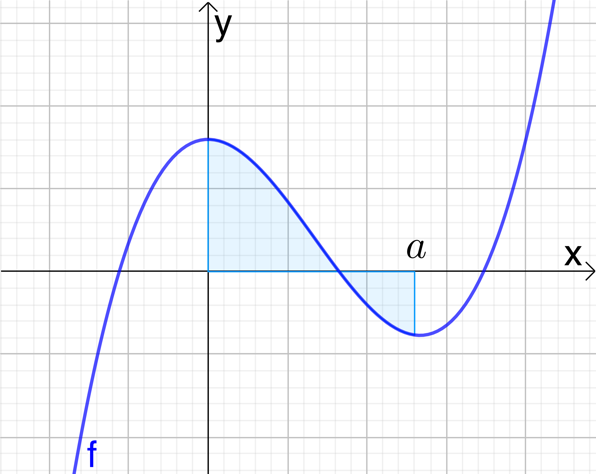
Gucken wir uns nochmal dieses GeoGebra Applet an, sehen wir, dass der Funktionswert der  Stammfunktion F(x) genau den Flächeninhalt in dem Intervall [0; a] angibt. 

Ist f eine Änderungsrate (wie z.B. eine Geschwindigkeit oder Zuflussrate), so erhält man den Bestand  (zurückgelegter Weg, Zuflussmenge) zu einem bestimmten Zeitpunkt a, indem man den orientierten Flächeninhalt unter dem Graphen im Intervall [0; a] bestimmt. Man schreibt hierfür:

 

 

 

 

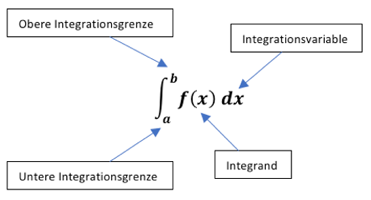
(Lies: Das Integral von f(x) in den Grenzen von 0 bis a)

 

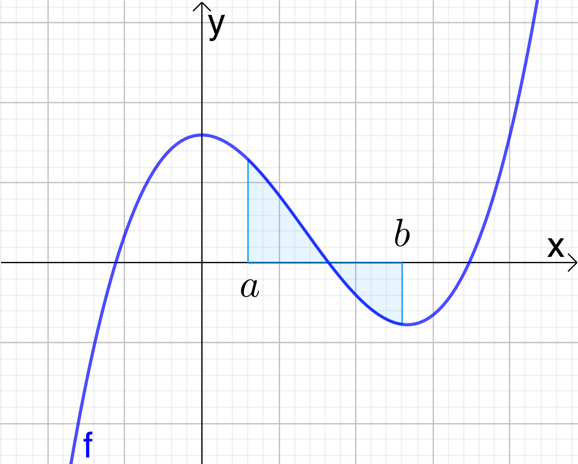
Möchte man nun z.B. die Zuflussmenge in einem Wasserbecken in einem Zeitraum von der 3. bis zur 6. Minute berechnen, muss man die Integrationsgrenzen entsprechend wählen. Es sind somit beiden Grenzen von 0 verschieden.

Allgemein bezeichnet also das Integral den orientierten Flächeninhalt unter dem Graphen der Funktion f im Intervall [a; b].

 

 

 

 

 

 

 

 

 

 

(Lies: Das Integral von f(x) in den Grenzen von a bis b)