Einführung in die Integralrechnung
Wir können bisher das Integral im Integral in den Grenzen von 0 bis a berechnen, in dem wir den Funktionswert der Stammfunktion an der Stelle a Bestimmen.
Nun möchte wir das Integral im Intervall von a bis b bestimmen.
Klicken sie nacheinander die Kontrollkästchen an und überlegen sie, wie man das Integral in den Grenzen von a bis berechnen kann.
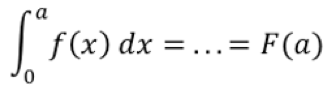
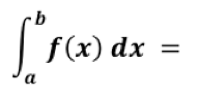
Ist F eine beliebige Stammfunktion von f, so gilt der Hauptsatz der Differential- und Integralrechnung. Er gibt den orientierten Flächeninhalt unter der Funktion f(x) in den Grenzen a und b an.