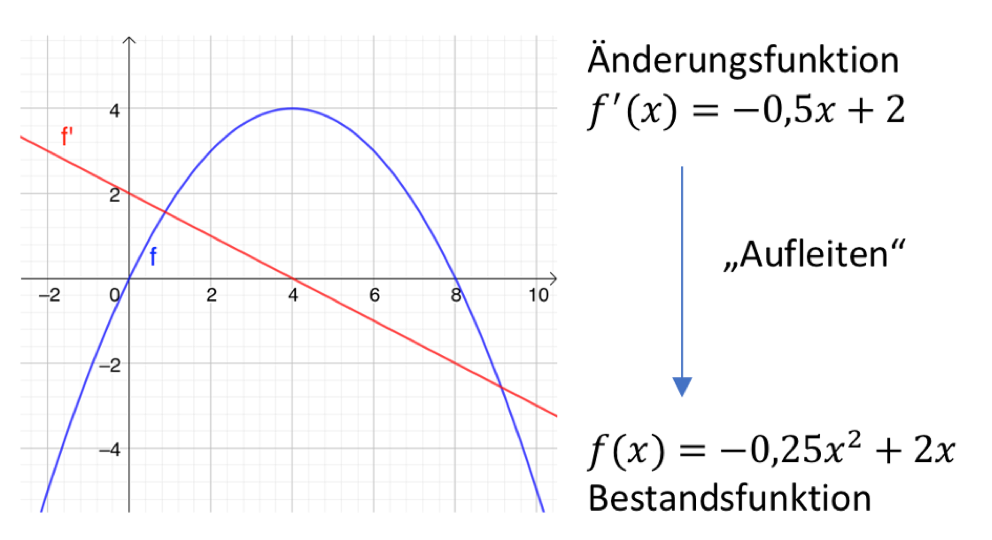
In den vorangegangenen Übungen hast du dir erarbeitet, wie man die Funktionsgleichung der Bestandsfunktion bestimmen kann. Ist also ein Funktionsterm y=f’(x) der Änderungsfunktion gegeben, so gelingt es in vielen Fällen die Bestandsfunktion zu rekonstruieren, indem man das Ableiten umkehrt. Man sucht also einen Term f(x), dessen Ableitung f’(x) ergibt.

Der beim „Aufleiten“ (Vorsicht, dies ist kein mathematischer Fachbegriff) von f’(x) gefundene Term f(x) ist nicht eindeutig, denn auch g(x)=f(x)+c mit einer Konstanten c hat als Ableitung die Funktion f’(x). Die Konstante c wird erst durch die Anfangsbedingung („wie groß ist der Anfangsbestand f(0)“) eindeutig festgelegt.