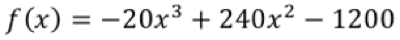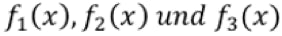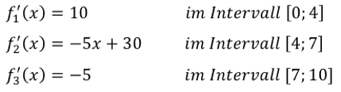Einführung in die Integralrechnung
1. Wende den Hauptsatz der Differenzial- und Integralrechnung an und bestimme die folgenden Integrale.
Bei Aufgabe c) hat sich ein Tippfehler eingeschlichen. Es heißt sin(x).
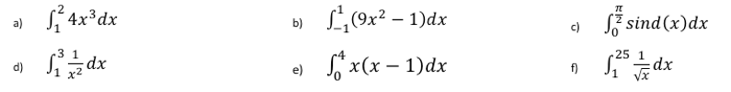
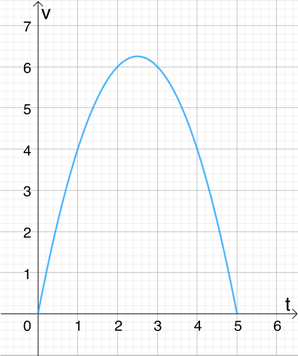
2. Die Zuflussgeschwindigkeit von Wasser in ein Becken wird durch die Funktion v(t)=5t-t2 in der Zeit von t=0 bis t=5 modelliert.
Dabei wird v in m3/h angegeben und t in Stunden.
a) Beschreibe, wie sich die Zuflussgeschwindigkeit mit der Zeit ändert.
b) Wie lautet die Funktionsgleichung, mit der man die Wassermenge darstellen kann, die in der Zeitspanne von 0bis t zugeflossen ist?
c) Berechne, welche Wassermenge in den ersten 4 Stunden zugeflossen ist.
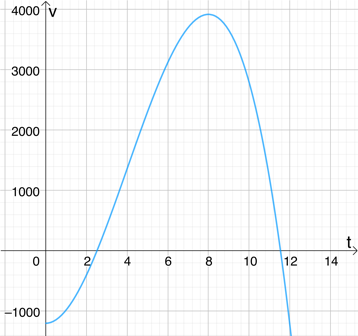
3. Gewinnentwicklung
Die Gewinnentwicklung in € pro Woche beim Verkauf eines neuen Produktes wird in den ersten 12 Monaten mit der Funktion. beschrieben(siehe Diagramm). Die Zahlen auf der Zeitachse geben jeweils das Ende das entsprechenden Monats an.
a) Beschreibe den Verlauf der Gewinnentwicklung
b) Ermittle den Gesamtgewinn in den ersten viert Monaten und vom Beginn des zweiten Monats bis zum Ende des zehnten Monats.
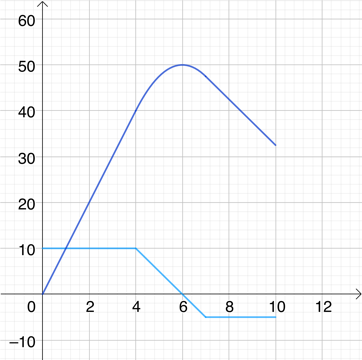
4. Die Funktionsterme für die Zuflussrate f’(x) sind hier abschnittsweise notiert:
Wie sehen die Terme der zugehörigen Bestandsfunktionen in den einzelnen Abschnitten aus? Zeige , dass diese an den Übergangsstellen der Intervalle jeweils die gleiche Steigung haben.
Aus Mathematik - Neue Wege - Analysis II, S. 156 und 158.